Trọng tâm chính là kiến thức quan trọng trong toán học. Trong một hình có rất nhiều điểm và mỗi điểm có một tên gọi khác nhau, trọng tâm cũng là một trong các điểm đó. Vậy trọng tâm là gì? Trọng tâm của tam giác được xác định thế nào? Hãy theo dõi bài viết sai đây các bạn nhé!
Trọng tâm là gì?
Theo từ điển Hán Việt, trọng tâm là 重心: 重 là trọng, “sức nặng” và 心 là tâm, “phần ở giữa”.
Danh từ của trọng tâm:
Vật lý học: Điểm đặt của trọng lực tác dụng vào một vật.
Toán học: Giao điểm của ba trung tuyến trong một tam giác.
Điểm quan trọng nhất: Trọng tâm công tác, trọng tâm của công việc, trọng tâm tam giác, trọng tâm tứ giác, trọng tâm con đường,…
Trong tiếng Anh, trọng tâm là center, ví dụ: center of weight, barycenter, barycentre.
Tiếng Tây Ban Nha: baricentro gđ….
Trọng tâm của tam giác là gì?
Trọng tâm trong tam giác là giao điểm của ba đường trung tuyến xuất phát từ ba đỉnh.
Trọng tâm tam giác chính là giao điểm của ba đường trung tuyến đi từ ba đỉnh của hình tam giác. Có nghĩa là khi ta kẻ từ ba đỉnh tam giác sang cạnh đối diện sẽ cho ba đường trung tuyến và nó sẽ gặp nhau tại một điểm, điểm trùng đó được gọi là trọng tâm của tam giác.
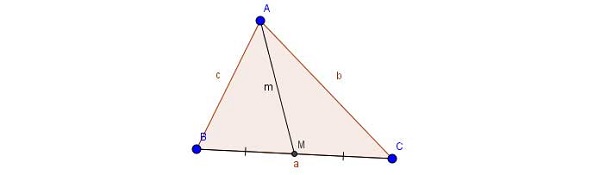
Nói cho các bạn học dễ hình dung thì với hình tam giác ABC. Chúng ta kẻ từ đỉnh A sang cạnh đối diện được trung điểm D, kẻ từ B sang được trung điểm E, kẻ từ C sang được trung điểm F. Theo đó, ba điểm này sẽ giao nhau tại điểm G nên chúng ta gọi G là điểm trọng tâm.
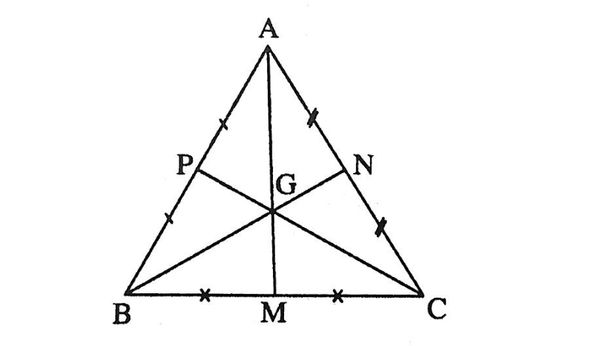
Tính chất trọng tâm của tam giác
Để xác định trọng tâm của một tam giác ta thực hiện:
Cách 1:
Tìm trung điểm M của BC sao cho MC = MB
Nối A với M ta được đường trung tuyến AM.
Tương tự với các đường trung tuyến còn lại.
Giao 3 đường trung tuyến là điểm G. Suy ra G chính là trọng tâm tam giác ABC.
Cách 2:
Tìm trung điểm M của BC sao cho MC = MB
Nối A với M ta được đường trung tuyến AM.
Trên đoạn thẳng AM lấy điểm G sao cho:
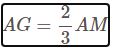
Vậy theo tính chất trọng tâm ta có G chính là trọng tâm tam giác ABC.
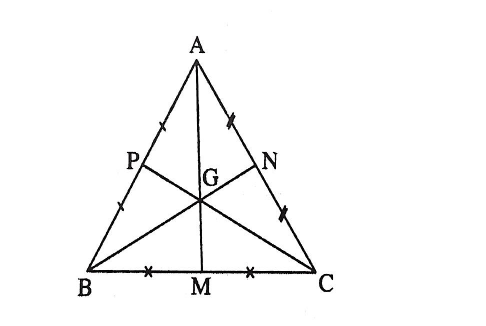
Cho tam giác ABC có AM, BN, CP lần lượt là ba đường trung tuyến tại đỉnh A, B, C. Ta có giao của ba đường trung tuyến là điểm G. Vậy G là trọng tâm của tam giác ABC.
Trọng tâm của các hình học đặc biệt
Trọng tâm tam giác vuông
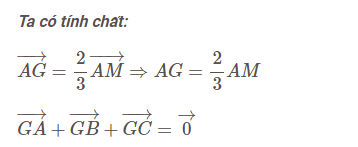
Tam giác ABC vuông tại B, từ B vẽ đường trung tuyến BA, vì BA là đường trung tuyến của góc vuông nên: BA = 1/2 CD=AD = AC.
Vậy tam giác ADB và tam giác ABC lần lượt cân tại A
Trọng tâm tam giác cân
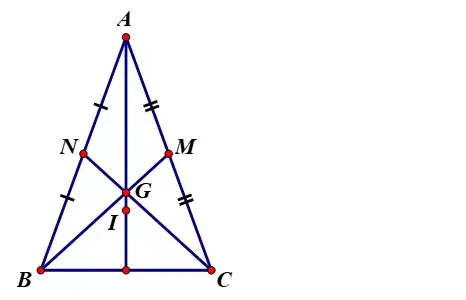
Cho tam giác ABc cân tại A, G là trọng tâm tam giác ABC. Vì tam giác cân tại A, nên AG vừa là đường trung tuyến, vừa là đường cao và là đường phân giác cùa tam giác ABC.
Hệ quả ta được:
AG vuông góc với BC.
Trọng tâm tam giác đều
Cho tam giác ABC đều, G là giao điểm ba đường trung tuyến. Theo tính chất của tam giác đều ta có G vừa là trọng tâm, trựa tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
Trọng tâm tứ diện
Ta có G là trọng tâm tứ diện ABCD. Trọng tâm tứ diện là giao điểm của bốn đường thẳng nối đỉnh và trọng tâm của tam giác đối diện.
Cách xác định trọng tâm của tam giác
Tính chất trọng tâm của tam giác là khoảng cách từ trọng tâm đến ba đỉnh của tam giác.
Trọng tâm của tam giác cân cũng sẽ được xác định như những loại bình thường. Thế nhưng đây là dạng tam giác đặc biệt nên chúng ta sẽ xét nó cân tại điểm A của tam giác ABC.
Trọng tâm của tam giác vuông cũng sẽ được xác định tương tự như những loại tam giác trên. Thế nhưng bạn cũng lưu ý là vuông tại A của tam giác ABC.
Trọng tâm của tam giác vuông cân cũng xác định như trên. Ta cũng xét thêm điểm vuông tại A của tam giác vuông cân ABC.
Những kiến thức về đường trung tuyến của tam giác
Trung tuyến là gì?
Trong hình học, trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba đường trung tuyến. Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau. Trong hình học không gian, khái niệm tương tự là mặt trung tuyến trong tứ diện.
Đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó. Đường trung tuyến được định nghĩa rõ ràng và ngắn gọn như sau: Đường trung tuyến 1 đoạn thẳng là một đường thẳng sễ đi qua trung điểm của đoạn thẳng đó.
Đường trung tuyến của tam giác là gì?
Trong hình học thì đường trung tuyến của một tam giác được định nghĩa là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác sẽ có 3 đường trung tuyến.
Trung tuyến 1 tam giác là một đoạn thẳng nối từ đỉnh tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác sẽ có ba trung tuyến.
Tính chất đường trung tuyến trong tam giác
Ba đường trung tuyến của tam giác sẽ cùng đi qua một điểm. Điểm đó sẽ có khoảng cách với đỉnh bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó. Giao điểm của ba đường trung tuyến chúng ta gọi là trọng tâm.
Tam giác vuông là tam giác mà nó có góc là góc vuông (90 độ). Đường trung tuyến của tam giác vuông sẽ mang các tính chất của một đường trung tuyến tam giác. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Suy ra nếu một tam giác đường trung tuyến ứng với một cạnh bằng nửa cạnh đó, tam giác ấy khẳng định sẽ là tam giác vuông.
Tam giác ABC vuông ở B, độ dài đường trung tuyến BM sẽ bằng MA, MC và bằng 1/2 AC
Ngược lại nếu BM = ½ AC thì tam giác ABC sẽ vuông ở B.
Ba đường trung tuyến của tam giác khi cùng đi qua điểm, điểm đó sẽ cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy. Giao điểm khi ba đường trung tuyến đi qua một điểm được gọi là trọng tâm.
Giao điểm của ba đường trung tuyến gọi là trọng tâm
Giả thuyết : G là trọng tâm của tam giác ABC
Kết luận : AG/AD=BG/BE=CG/CF=2/3
Đồng quy tại 1 điểm
Ba đường trung tuyến của tam giác đồng quy tại 1 điểm. Điểm đó được gọi là trọng tâm của tam giác. Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Chia ra diện tích của các tam giác bằng nhau
Mỗi trung tuyến chia diện tích của tam giác thành hai phần bằng nhau. Ba trung tuyến chia tam giác thành sáu tam giác nhỏ với diện tích bằng nhau.

Qua bài viết trên các bạn đã biết trọng tâm là gì và cách xác định trọng tâm của tam giác thế nào rồi đúng không? Hy vọng bài viết trên có thể giúp ích được cho bạn. Trọng tâm rất dễ nhầm lẫn với các điểm khác nên bạn hãy chú ý khi xác định nhé!